| I am completing my PhD at the Lorentz Institute at Leiden University, in the Soft Condensed Matter Theory Group of Vincenzo Vitelli. I took my first degree in Mathematics at the University of Cambridge many years ago and completed the Masters in Physics at Leiden University in 2014. Before returning to academia, I pursued a varied career in business, with roles in finance in government, pharmaceuticals, financial services and mining in the UK, Hong Kong, Poland and the Netherlands. |

|
Topological mechanics
Swimming topological mechanical chains
|
3-rotor flipper |
Bodies move through fluids by swimming, i.e., by changing their shape through a periodic stroke.
Newton's third law of action and reaction presents a challenge to all swimmers: the net force which the body exerts on the fluid is zero. This problem is particularly acute in viscous fluids since there is no possibility to use inertia to "glide" because inertia is not relevant to the motion.
Instead, the body's motion is controlled by the sequence of steps executed in the swimming stroke.
A body moves despite not being able to exert a net force on the fluid by deforming its shape and taking advantage of the anisotropy of the reactive force.
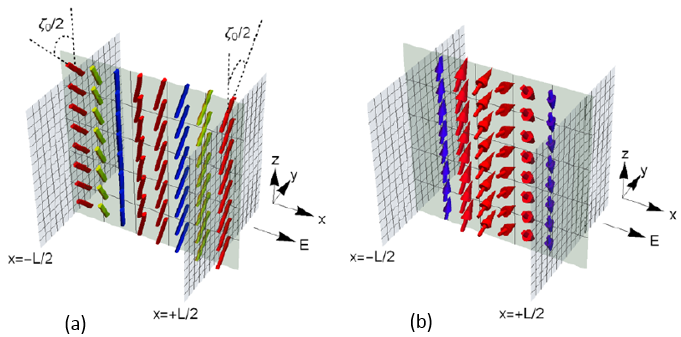
Topological mechanical chains have different phases whose kinematics can be characterised by different dynamical winding numbers W. In the spinner phase, each rotor winds once through 2π in one cycle which returns the chain to its starting configuration (W=1). In the flipper phase on the other hand, rotors in the bulk oscillate from side to side while at the edge rotors describe a bigger movement but W=0 for all rotors in the chain. At the transition between spinner and flipper, both phases are accessible to the chain but the phase selected by the chain is the superspinner phase shown opposite, which has dynamical winding number W=2. A natural question to ask is whether these chains can swim, and if so, how well? I show that the swimming result at low Reynolds number depends not only on the phase, but also on whether the number of rotors is odd or even, due to the presence of symmetries in the swimming stroke. It turns out that for the 3-rotor chains shown here, the spinner chain is unable to swim in the horizontal direction, whereas both the flipper and superspinner chains can. |
Active matter
Geometry of thresholdless active flow in nematic microfluidics
 |
The liquid crystal in the display of your watch is static: it does not
flow as long as time displayed does not change. This is because the
long, cigar-shaped molecules of which it
is composed are dead. What happens if we put live swimmers into such a
medium? This can now be done: non-toxic liquid crystals have been made,
and live, swimming bacteria put in them. Does this make the liquid
crystal as a whole flow?
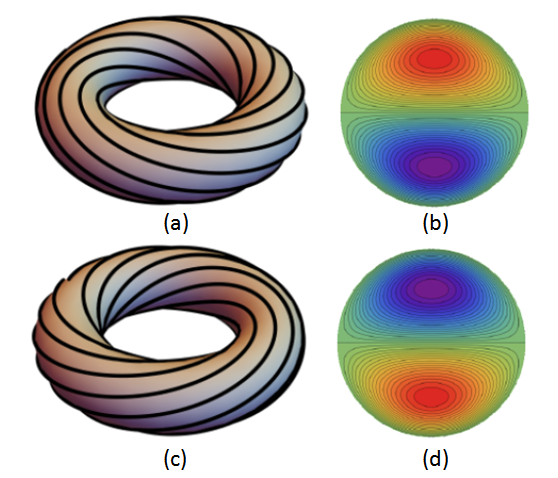
The answer to this question has long been known to depend on the configuration of the liquid crystal. In nematic liquid crystals, the molecules "like" (i.e., have lowest energy) if they line up with their axes parallel. In this uniform state, it's already known that the density of swimmers must exceed some non-zero critical density before the liquid crystal will flow. |
However, liquid crystal display technology distorts liquid crystals into spatially non-uniform configurations. In some of these, the liquid crystal will start to flow as soon as any non-zero density of swimmers is placed in it; we call this "thresholdless" flow. In others, there continues to be critical threshold density that must be exceeded before flow occurs.
Until now, there has been no general criterion for determining which distortions lead to thresholdless flow, and which do not. In our work, we provide such a general criterion, which will make it possible to design microscopic "pumps" in which the work of pumping is done by bacteria, without human intervention, and without moving parts. We also calculate the flow that occurs for low density of swimmers in such thresholdless conditions.
Paper
Geometry of thresholdless active flow in nematic microfluidics
