







We are cosmologists, in other words we use physics to study the Universe, how it started and evolved into the structure that we observe around us. With the evolution of the universe spanning a vast range of energies and scales, cosmological observables can shed light on virtually any particle physics model as well as on any theory of gravity. Our passion and interests are in using the array of cosmological data available to us to test fundamental physics. Through the past years we have been involved both in theoretical and observational aspects of this endeavor, with a particular focus on tests of gravity on cosmological scales. We are a very active part of the Euclid mission and have recently started a Gravitational Waves Cosmology program jointly with the gravitational waves group at GRAPPA (UvA). See below for a sample of recent works.
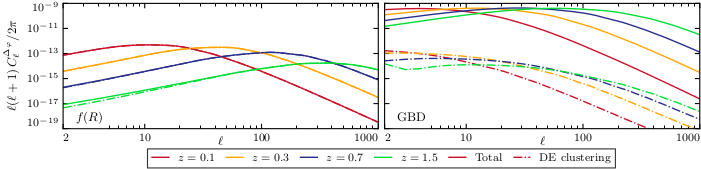
Gravitational Wave (GW) and multi-messenger measurements with ongoing and upcoming experiments, will undoubtedly provide a much needed new frontier, fully complementary to the more traditional cosmological probes offered by Large Scale Structure. GWs can be used as standard sirens, and provide a calibration-free estimate of H_0. With the upcoming missions it will be possible to measure H_0 at percent level as well as reconstruct the expansion history over a, yet unexplored redshift range (as we show in one of the papers below). Furthermore, the propagation of GWs through the expanding Universe provide a rich testing bed for dark energy models and extended theories of gravity; highly competitive bounds already came from the constraint on the speed of propagation of GWs; but a lot more can be achieved in the coming years, studying the interaction between GWs and the inhomogeneities along their path. In some preliminary work we explore how cross-correlations of GW sources with galaxy catalogues, weak lensing of galaxies and the Cosmic Microwave background, as well as with Supernovae catalogues will offer innovative and powerful ways of testing gravity and unveiling the nature of DE.
H0 from binary black holes .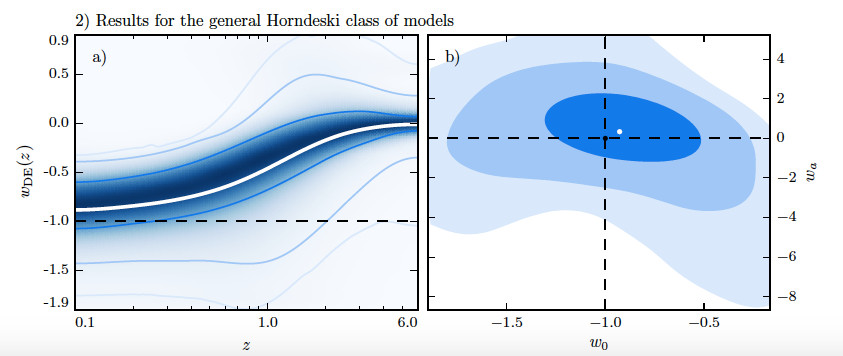
Constraining the DE equation of state, wDE, is one of the primary science goals of ongoing and future cosmological surveys. In practice, with imperfect data and incomplete redshift coverage, this requires making assumptions about the evolution of wDE with redshift z. These assumptions can be manifested in a choice of a specific parametric form, which can potentially bias the outcome, or else one can reconstruct wDE(z) non-parametrically, by specifying a prior covariance matrix that correlates values of wDE at different redshifts. Using the stability conditions built-in in EFTCAMB, and sampling over a large ensemble of models within the EFT framework we construct the theoretical prior covariance for the effective DE equation of state predicted by general scalar-tensor theories with second order equations of motion (Horndeski theories), as shown in the left bottom panel of the Figure. This is achieved by generating a large ensemble of possible scalar-tensor theories using a Monte Carlo methodology, including the application of physical viability conditions. We also separately consider the special sub-case of the minimally coupled scalar field, or quintessence (left upper panel). The prior shows a preference for tracking behavior in the most general case. Given the covariance matrix, theoretical priors on parameters of any specific parametrization of wDE(z) can also be readily derived by projection. In the right panels we show the projection of the covariance matrix on the popular CPL parametrization.
JCAP07(2019)042.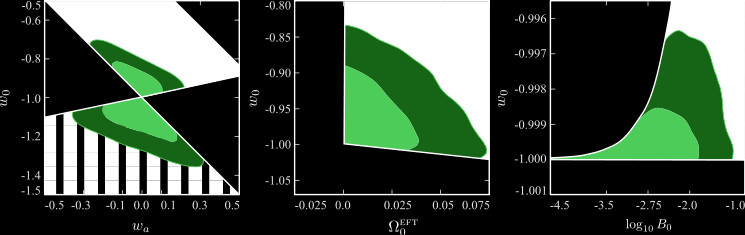
Physics remains the guiding principle in the agnostic exploration of DE! Since the EFT framework is based on an action, it is possible to derive in a very general form a set of conditions on the EFT functions to ensure that the underlying theory is theoretically consistent; i.e. we require our theory to be cosmologically viable and to be stable, e.g. do not develop ghost or gradient instabilities. It is possible to perform an EFT diagnostic before specializing to any model, derive a set of conditions on the EFT functions and translate them into theoretical priors included in the analysis pipeline via a stability module attached to EFTCAMB. This Figue shows the big effect that these conditions can have on the theory parameter space: in all three plots the white regions are excluded by stability conditions. As a result, we are left with a much reduced parameter space to sample and the comparison with data becomes significantly more efficient and informative. The overall constraining power can also increase significantly.
10.1103/PhysRevD.96.063524.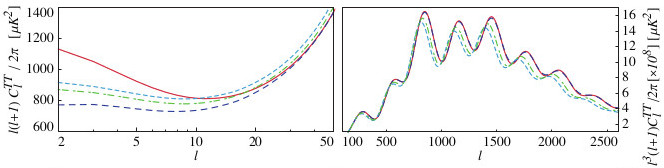
We have performed a careful and comprehensive implementation of the effective field theory (EFT) of cosmic acceleration into CAMB. The result, EFTCAMB, is a powerful tool which can be used to investigate the implications of the different EFT operators on linear perturbations, in an agnostic approach to tests of gravity, as well as to study perturbations in any specific single field dark energy or modified gravity model. This framework has several crucial virtues (e.g. it evolves the full dynamics of perturbations on all linear scales) and overcomes some of the limitations of previous approaches, offering a significantly extended applicability as well as a more accurate modeling which will be crucial in view of the percent level accuracy of future measurements. In a series of papers we present the numerical implementation, illustrate its use to extract theoretical predictions for power spectra in a very broad range of models and put it at work with current data.
Mon.Not.Roy.Astron.Soc. 459 (2016) no.4, 3880-3889.
In general relativity the metric outside a compact source will be static no matter what the dynamics of the source is as long as it obeys spherical symmetry. This may not be the case any more in models of gravity where the Birkhoff’s theorem ceases to hold. I have investigated one of the consequences of the violation of the latter theorem, namely scalar radiation from chameleon shielded regions. Chameleons are scalar fields characterized by a profile that depends on the local matter density, as a consequence of their coupling to matter fields, and can screen themselves from local tests of gravity. The very same coupling allows a radially pulsating mass to directly propagate a disturbance into the space surrounding it with the radiation spectrum carrying characteristic imprints depending on whether the source is successfully screened or not. There are several interesting related scenarios; for instance, energy could be drained from binary black holes faster than in GR; the ripples in the Chameleon profile would induce time-variations of masses and fundamental coupling constants; the hydrodynamics of compact objects, in particular the core collapse, could be significantly modified. We have studied this in 10.1103/PhysRevLett.106.251101 and are now resuming work on several different scenarios.









Oort Building
Niels Bohrweg 2
2333CA Leiden
The Netherlands
Phone: (0031) 71-5275540
Email: silvestri@lorentz.leidenuniv.nl
Here you can find the list of publications from the PI.
A look at Hubble speed from first principles.
arXiv:2011.10559
Detecting Dark Energy Fluctuations with Gravitational Waves.
arXiv:2007.13722
Accurate and precision Cosmology with redshift unknown gravitational wave sources.
arXiv:2007.02943
Strong Lensing Time Delay Constraints on Dark Energy: a Forecast.
JCAP 04 (2020) 057
Generalized Brans-Dicke theories in light of evolving dark energy.
Phys.Rev.D 101 (2020) 4, 043518
Reconstruction of the Dark Energy equation of state from latest data: the impact of theoretical priors.
JCAP 1907 (2019) 042
MGCAMB with massive neutrinos and dynamical dark energy.
JCAP 1905 (2019) 001
Splashback radius in symmetron gravity.
Phys.Rev. D99 (2019) no.6, 064030
The role of the tachyonic instability in Horndeski gravity.
JCAP 1902 (2019) 029
Phenomenology of Large Scale Structure in scalar-tensor theories: joint prior covariance of wDE, Σ and μ in Horndeski.
Phys.Rev. D99 (2019) no.2, 023512
Large-scale structure phenomenology of viable Horndeski theories.
Phys.Rev. D97 (2018) no.4, 043519.
Do current cosmological observations rule out all Covariant Galileons?.
Phys.Rev. D97 (2018) no.6, 063518.
Comparison of Einstein-Boltzmann solvers for testing general relativity.
Phys.Rev. D97 (2018) no.2, 023520.
Priors on the effective Dark Energy equation of state in scalar-tensor theories.
Phys.Rev. D96 (2017) no.8, 083509.
On nonlocally interacting metrics, and a simple proposal for cosmic acceleration.
JCAP 1803 (2018) no.03, 048.
Impact of theoretical priors in cosmological analyses: the case of single field quintessence.
Phys.Rev. D96 (2017) no.6, 063524.
What can cosmology tell us about gravity? Constraining Horndeski gravity with $\Sigma$ and $\mu$.
Phys.Rev. D94 (2016) no.10, 104014.
Testing Hu–Sawicki f(R) gravity with the effective field theory approach.
Mon.Not.Roy.Astron.Soc. 459 (2016) no.4, 3880-3889.
An Extended action for the effective field theory of dark energy: a stability analysis and a complete guide to the mapping at the basis of EFTCAMB.
JCAP 1607 (2016) no.07, 018.
Kinetic Sunyaev-Zel’dovich effect in modified gravity.
Phys.Rev. D93 (2016) no.6, 064026.
Testing deviations from ΛCDM with growth rate measurements from six large-scale structure surveys at $z = $0.06–1.
Mon.Not.Roy.Astron.Soc. 456 (2016) no.4, 3743-3756.
Hořava Gravity in the Effective Field Theory formalism: From cosmology to observational constraints.
Phys.Dark Univ. 13 (2016) 7-24.
Exploring massive neutrinos in dark cosmologies with $\scriptsize{EFTCAMB}$/ EFTCosmoMC.
Phys.Rev. D91 (2015) no.6, 063524.
Measuring the speed of cosmological gravitational waves.
Phys.Rev. D91 (2015) no.6, 061501.
EFTCAMB/EFTCosmoMC: Numerical Notes v3.0.
[arXiv:1405.3590 [astro-ph.IM]].
Effective Field Theory of Cosmic Acceleration: constraining dark energy with CMB data.
Phys.Rev. D90 (2014) no.4, 043513.
Effective Field Theory of Cosmic Acceleration: an implementation in CAMB.
Phys.Rev. D89 (2014) no.10, 103530.
Observable physical modes of modified gravity.
Phys.Rev. D89 (2014) no.8, 083505.
Effective Field Theory of Dark Energy: a Dynamical Analysis.
JCAP 1402 (2014) 026.
New Constraints On The Dark Energy Equation of State.
Phys.Rev. D88 (2013) 043515.
Practical approach to cosmological perturbations in modified gravity.
Phys.Rev. D87 (2013) no.10, 104015.
Practical solutions for perturbed f(R) gravity.
Phys.Rev. D86 (2012) 123503.
Parametrised modified gravity and the CMB Bispectrum.
Phys.Rev. D86 (2012) 063517.
Cosmological tests of General Relativity: a principal component analysis.
Phys.Rev. D85 (2012) 043508.
Scalar radiation from Chameleon-shielded regions.
Phys.Rev.Lett. 106 (2011) 251101.
Modifying gravity: Cosmic acceleration and the large scale structure of the universe.
By Alessandra Silvestri.
Probing modifications of General Relativity using current cosmological observations.
Phys.Rev. D81 (2010) 103510.
How to optimally parametrize deviations from General Relativity in the evolution of cosmological perturbations?.
Phys.Rev. D81 (2010) 104023.
New constraints on parametrised modified gravity from correlations of the CMB with large scale structure.
JCAP 1004 (2010) 030.
Reconstructing the Peculiar Velocity of the Local Group with Modified Gravity and 2MASS.
Mon.Not.Roy.Astron.Soc. 401 (2010) 1219-1230.
Cosmological Tests of General Relativity with Future Tomographic Surveys.
Phys.Rev.Lett. 103 (2009) 241301.
Approaches to Understanding Cosmic Acceleration.
Rept.Prog.Phys. 72 (2009) 096901.
Non-Gaussian Signatures from the Post-inflationary Early Universe.
Phys.Rev.Lett. 103 (2009) 251301.
Searching for modified growth patterns with tomographic surveys.
Phys.Rev. D79 (2009) 083513.
The pattern of growth in viable f(R) cosmologies.
Phys.Rev. D77 (2008) 023503, Erratum: Phys.Rev. D81 (2010) 049901.
Dynamics of Linear Perturbations in f(R) Gravity.
Phys.Rev. D75 (2007) 064020.
Modified-Source Gravity and Cosmological Structure Formation.
New J.Phys. 8 (2006) 323.
Chiral anomalies via classical and quantum functional methods.
Int.J.Mod.Phys. A20 (2005) 5009-5036.