Universal algebraic velocity relaxation of uniformly tranlating
as well as pattern forming pulled fronts
In almost all fields of the natural sciences, we encounter propagating fronts which separate regions of different behavior of the system. The example most familiar from the daily weather forecast on television are the weather fronts separating, e.g., regions of cold air from hot air, dry sunny weather from rainy zones, etc. Just like the propagation of such fronts dominates most of the weather changes, so do propagating fronts or interfaces play an important role in the spreading of an epidemic, the way in which nerve pulses or chemical reactions spread, the propagation of sparks in discharges, the pearling instability of membranes after laser quenching, or the instability that makes the wires of bridges like the Golden Gate vibrate and wistle in the wind. In fact, in many pattern forming systems the dynamics naturally can be divided up into domains or different bulk phases separated by interfaces, domain walls or fronts; understanding the behavior of front propagation is then a crucial ingredient for analyzing the dynamics.
Except for the weather fronts, the common denominator of all the fronts mentioned above is that they are examples of fronts that propagate into an unstable state: e.g., the pearling instability of membranes arises from the fact that membrane itself has become unstable after the surface tension of the membrane has been altered with a laser pulse. Other experimental examples of fronts which propagate into an unstable state have been studied in Rayleigh-Benard cells and in the Taylor-Couette system. But the physics of front propagation into unstable states plays a role in many systems: in the discharges mentioned earlier, in a mean-field treatment of ballistic deposition, in chemical waves and nerve pulses, in error propagation, in the propagation and stability of nonlinear pulse solutions in binary convection, etc.
The simplest type of fronts are those which separate two homogeneous states, one of which is stable and one of which is unstable. But there are also so-called pattern-forming fronts, which either generate a coherent pattern, like a periodic state, or a chaotic state. We show two examples of such pattern forming fronts in Fig. 1. The one on the left is obtained from a simulation of the so-called Swift-Hohenberg equation; clearly, this is a coherent pattern-forming front as it leads to a well-defined periodic state. The one on the right generates a incoherent chaotic state - it is obtained from simulations of the so-called Complex Ginzburg-Landau equation.
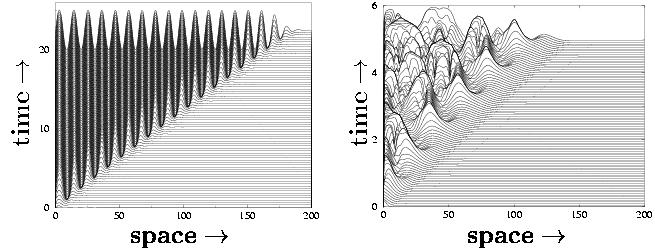
Figure 1: Two examples of fronts propagating into
an unstable
state. The dynamics is shown by plotting the fronts at successive
moment one above the other. The front on the left gives rise to a
periodic state and is obtained from a simulation of the
Swift-Hohenberg
equation, the one on the right creates a chaotic
state, and is obtained from a simulation of the Complex
Ginzburg-Landau equation. Nevertheless, the way in which these fronts "mature"
(i.e. approach their asymptotic speed and front shape) is given by one
and the same formula.
Although fronts of this type have been studied already since the nineteen thirties when Fisher studied the spreading of an epidemic, Ute Ebert and I recently discovered a remarkable thing: the propagation mechanism of for a large class of such fronts is extremely simple and surprisingly universal. In an unstable state, even a small perturbation will grow and spread due to a type of snowball or avalanche effect. For almost any dynamical model the asymptotic spreading speed v* can be calculated explicitly from the underlying equations in terms of the dispersion relation of the unstable fourier modes. This is basically due to the fact that the asymptotic spreading speed of the linearized dynamical equations can be obtained from a saddle point expansion of the Green's function. It has been known for some time now (see the references in the papers cited below) that while the various fronts which propagate into an unstable state may all describe very different behavior, quite often their asymptotic front speed is simply equal to this linear spreading speed: it is as if the full front, with all its complicated nonlinear or chaotic behavior, is "being pulled along" by the leading edge of the front. The rest of the front just follows along. For this reason, such fronts are sometimes referred to as "pulled fronts". Pulled fronts occur in particular when the nonlinearities in the dynamical equations mainly damp the growth, and hence lead to saturation - the other class of fronts are so-called "pushed" fronts; these propagate faster than the linear spreading speed v*.
In passing, we note that when I worked on front propagation some ten years ago (see the paper listed below), I used the words linear marginal stability for the regime that above is referred to as pulled and nonlinear marginal stability for the regime we now call pushed. These notions are often used in the literature these days. Ute Ebert and I now prefer the names pulled and pushed (which were introduced long ago by Stokes in a biomathematics paper) since they are closer to the intuitive notion of fronts which are either "being pulled along" by the linear growth and spreading, or "being pushed" from behind by the nonlinear region.
The recent surprising discovery of Ute Ebert and myself is that the above picture can be made into a full dynamical theory which goes far beyond the statement that the asymptotic speed of pulled fronts is equal to the linear spreading speed: our analysis shows that every pulled front relaxes to its asymptotic speed algebraically with time in a universal way: if we track a so-called level line, the point in a space-time diagram where the dynamical field reaches a fixed value, then the velocity v(t) of this point is given by
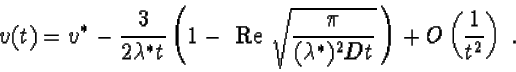 |
(1) |
Besides the asymptotic spreading speed v*, also the other constants in this expression, lambda* and D can be calculated explicitly for a given problem. For simple fronts which asymptotically propagate uniformly and which hence lead to a homogeneous rather than a patterned state, D is real, but in its above form, the equation holds for all types of pulled fronts. For pattern forming fronts, there is an analogous expression for the power law relaxation of the phase. The first term of order 1/t was derived for the special case of the nonlinear diffusion equation ("Fisher equation") almost 20 years ago, and I proposed its general form in my 1989 paper listed below. The exact 1/t3/2 term is new even for the nonlinear diffusion equation, but the most essential part of our analysis is the systematic derivation of this result for arbitrary dynamical equations that admit pulled fronts. Below is a table with the various equations for which we have shown explicitly that our results apply.
The above result is remarkably universal:
(i) It is independent of the precise initial conditions, provided they
are "sufficiently steep".
(ii) It is independent of the precise form of the equation, i.e.,
whether it is a partial differential equation, a difference equation, or an
equation with a memory or spatial kernel. The various equations that we have
studied explicitly to illustrate this, are listed in Table I below.
(iii) It is independent of the nonlinearities and of whether the front
is pattern-generating or not.
(iv) It is independent of which precise level line one follows, in
other words, independent of which precise "height" one tracks to measure the
velocity.
The above universal relaxation is just one of the important manifestations of the fact that the essential dynamics of pulled fronts occurs ahead of the front, not inside the nonlinear front region itself. A second manifestation of this shift is that the standard perturbation theory or the standard moving boundary approximation does not apply to pulled fronts. This is discussed in one of the papers with Ute Ebert below. It also suggests that fluctuating pulled fronts do not obey KPZ scaling. Further discussion of this point, and evidence that this picture is essentially correct, is given in the paper with Goutam Tripathy listed below. Finally, Andrea Rocco, Ute Ebert and I recently discovered that it also implies that pulled fronts in the presence of multiplicative noise exhibit subdiffusive behavior.
If you've read Animal Farm by George Orwell, you'll surely remember
that the animals in charge like to say "All animals are equal, but
some are more equal than others". With a wink at this famous line,
we summarize the remarkable universality of pulled fronts as "Some
fronts are more equal than others". As we wrote in the
laypaper
version of a talk at the 2000 APS March meeting:
Normally,
fronts relax very fast; it is as if, in
human
terms, "they mature very fast". But the way in which they mature is different
for each individual (front). Pulled fronts, however, mature very very slowly,
so slowly that it is as if they never really grow up. The second surprise is
that although they mature ("relax") very slowly, they do so in a universal
way:
all pulled fronts never seem to fully reach their adulthood, but the way they
go through their teenage life and early adulthood is the same for all
of them!
| The EFK eq.:
|
|
|
| The streamer eqs.: |
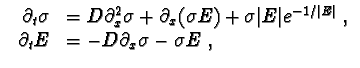
|
| A difference equation from kinetic theory: |
|
|
| A second order extension F-KPP eq.: |
|
|
| An equation with a memory kernel:
|
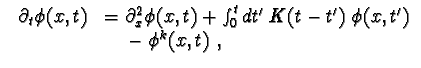 |
| Finite difference versions of the F-KPP eq. like:
|
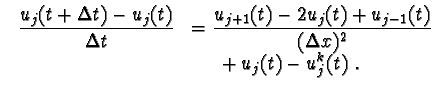 |
Table showing the various equations discussed in our long paper with Ute Ebert, and to which our universal power law relaxation formula for pulled fronts apply. These equations all admit uniformly traveling front solutions; pattern forming fronts are studied in the paper with Kees Storm.
Wim van Saarloos
March 9 2000
Relevant papers:
U. Ebert and W. van Saarloos, Front propagation into
unstable states: universal algebraic convergence towards
uniformly pulled fronts, revised version under review
for Physica D, March 2000
(ps file,
pdf file).
C. Storm, W. Spruijt, U. Ebert and W. van Saarloos, Universal
Algebraic Relaxation of Velocity and Phase in Pulled Fronts generating
Periodic or Chaotic States (submitted to Phys. Rev. E.)
pdf
file
U. Ebert and W. van Saarloos, Breakdown of the
standard Perturbation Theory and Moving Boundary
Approximation for "Pulled" Fronts, submitted to a
special issue of Physics Reports, December 1999.
(ps file)
G. Tripathy and W. van Saarloos, Fluctuation and
relaxation properties of pulled fronts: a possible scenario
for non-KPZ behavior, submitted to Phys. Rev. Lett.,
Jan. 2000. (ps file,
(pdf file)
A. Rocco, U. Ebert and W. van Saarloos, Subdiffusive
fluctuations of "pulled" fronts with multiplicative
noise, submitted to Phys. Rev. E, March 2000. (ps file)
A classic one of mine on the subject: W. van Saarloos, Front propagation into Unstable States II: Linear versus Nonlinear Marginal Stability and Rate of Convergence, Phys. Rev. A 39, 6367-6390 (1989).
I recently wrote a review of the field:: W. van
Saarloos, Front propagation into unstable states, to
appear in Physics Reports
(pdf file)
[Pattern formation] [Wim van Saarloos] [Instituut-Lorentz]